|
Политропическим называется процесс, в котором молярная теплоёмкость C остаётся постоянной. Уравнение политропического процесса имеет вид:
где
называется показателем политропы.
Молярная теплоёмкость – это физическая величина C, численно равная теплоте δQ, которую нужно сообщить одному молю вещества для изменения его температуры на 1 К в рассматриваемом термодинамическом процессе:
(M – молярная масса, m – масса газа).
Выражение (3) теперь можно записать в форме
или в интегральной форме
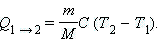
Таким образом, если количество тепла, полученное в некотором термодинамическом процессе 1→2 при m = const, прямо пропорционально разности температур ΔT = T2 – T1, то теплоёмкость газа постоянна и процесс является политропическим.
Первый закон термодинамики для любого равновесного процесса изменения состояния идеального газа имеет вид
Тогда из уравнения (5) имеем:
Связь между объёмом газа и его температурой в политропном процессе можно найти из выражения (1) и уравнения Клапейрона–Менделеева:
Дифференцируя последнее выражение, получим:
Тогда уравнение (6) примет вид:
Учитывая, что
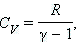 где где
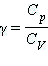 показатель адиабаты, получим: показатель адиабаты, получим:
или
Таким образом, если термодинамический процесс идеального газа действительно является политропным, то есть молярная теплоёмкость в ходе процесса не изменяется, то её величина рассчитывается по формуле (7).
В настоящей работе используется модель одноатомного газа (i = 3), поэтому в политропных процессах при n = –1 согласно выражению (7) молярная теплоёмкость C должна быть равна 16,6 Дж/моль∙К, а при n = –2 C = 15,2 Дж/моль∙К.
Частными случаями политропного процесса являются:
| 1) |
изотермический: n = 1, C = ±∞; |
| 2) |
изобарический: n = 0, C = Cp; |
| 3) |
изохорический: n = ±∞, C = CV; |
| 4) |
изохорический: n = γ, где
γ = Cp / CV, C = 0. |
|