|
Спектром электромагнитного излучения (ЭМИ) называется совокупность электромагнитных волн, излучаемых или поглощаемых атомами (молекулами) данного вещества.
Линейчатый спектр состоит из отдельных компонент (спектральных линий).
Спектральной линией называется электромагнитное излучение, испускаемое (или поглощаемое) атомом при переходе его электрона из одного стационарного квантового состояния в другое. Модели (классические) спектральной линии:
- гармоническая электромагнитная волна с частотой ν,
- поток фотонов с одной и той же энергией ЕФ = hν.
Расстояние между линиями (по шкале длин волн или частот) в линейчатом спектре много больше ширины линий. Такой спектр излучают атомарные газы.
Кроме линейчатого выделяют еще полосатый спектр, который излучают молекулярные газы, и сплошной спектр, излучаемый нагретыми твердыми телами.
Планетарная (орбитальная) модель атома: в центре атома расположено очень малое положительно заряженное ядро, вокруг которого по определенным (разрешенным) стационарным круговым орбитам движутся электроны, масса которых во много раз меньше массы ядра. При движении по орбите электрон не испускает электромагнитного излучения (ЭМИ). При поглощении ЭМИ (фотона) электрон переходит на более «высокую» разрешенную орбиту, на которой его энергия становится больше на величину ΔЕэл, равную энергии поглощенного фотона ЕФ. При обратном переходе электрон испускает фотон с такой же энергией ЕФ = |ΔЕэл|.
Квантовая модель атома отличается от планетарной в первую очередь тем, что в ней электрон не имеет точно определенного радиус-вектора (координаты) и вектора скорости, поэтому бессмысленно говорить о траектории его движения. Можно определить (и нарисовать) только границы области его преимущественного движения (орбитали).
Уравнение Шредингера для движения электрона в кулоновском поле ядра атома водорода используется для анализа квантовой модели атома. В результате решения этого уравнения получается волновая функция, определяющая плотность вероятности нахождения электрона вблизи данной точки. Она зависит не только от координаты 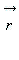 и времени t, но и от четырех параметров, имеющих дискретный набор значений и называемых квантовыми числами. Они имеют названия: главное, азимутальное, магнитное и магнитное спиновое.
и времени t, но и от четырех параметров, имеющих дискретный набор значений и называемых квантовыми числами. Они имеют названия: главное, азимутальное, магнитное и магнитное спиновое.
Более точное уравнение Дирака добавляет еще одно квантовое число, которое называется «магнитное спиновое». Его появление связывается с наличием у электрона некоторого внутреннего движения, называемого спиновым (коротко «спин»). При дальнейших исследованиях обнаружилось, что спиновым движением (спином) обладают и многие другие частицы.
Для модуля вектора момента импульса спинового движения
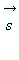 имеет место соотношение:
имеет место соотношение:
где s – спиновое квантовое число, которое у каждой частицы имеет только одно значение. Например, для электрона sэл = 1/2.
Аналогичные значения имеют спиновые квантовые числа протона и нейтрона. Но у фотона sФ = 1.
Главное квантовое число n может принимать целочисленные значения 1, 2, ... Оно определяет величину энергии электрона в атоме:
где ЕiH – энергия ионизации атома водорода (13,6 эВ). Азимутальное (орбитальное) квантовое число l определяет модуль момента импульса электрона при его орбитальном движении:
Оно принимает целочисленные значения l = 0, 1, 2, ... , n – 1.
Магнитное квантовое число ml определяет проекцию вектора момента импульса орбитального движения электрона Lz на направление внешнего магнитного поля 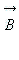 . Оно принимает положительные и отрицательные целочисленные значения, по модулю меньшие или равные l : . Оно принимает положительные и отрицательные целочисленные значения, по модулю меньшие или равные l :
где ml = 0, ±1, ±2, ..., ±l. Магнитное спиновое квантовое число 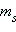 определяет проекцию вектора собственного момента импульса электрона (спина определяет проекцию вектора собственного момента импульса электрона (спина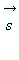 ) на направление внешнего магнитного поля ) на направление внешнего магнитного поля 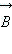 : :
принимает только два значения:
Вырожденными называются состояния электрона с одинаковой энергией.
Кратность вырождения равна количеству состояний с одной и той же энергией. Краткая запись состояния электрона в атоме:
- цифра, равная главному квантовому числу,
- буква, определяющая азимутальное квантовое число:
Буквенное обозначение для этого числа приведено в таблице:
Пример: Электрон в атоме имеет главное квантовое число n = 3, а азимутальное l = 2. Тогда краткая запись его состояния такова: «3d». Правило отбора азимутального квантового числа: Δl = ±1. Электрон в атоме может переходить только между состояниями, удовлетворяющему указанному правилу.
Спектральной серией называется совокупность линий излучения, соответствующих переходу электрона в атоме на один и тот же нижний уровень энергии. Для атома водорода
| Серия |
Лаймана |
Бальмера |
Пашена |
Брэкета |
| Переходы |
|
|
|
|
|